Verification and Synthesis of Complete Test Generation Algorithms for Finite State Machines (Tirage aléatoire uniforme dans une collection dynamique de chemins)
Exposé repris d'une présentation a MTV2
Personnes présentes
- Frédéric Boulanger
- Nicolay Kosmatov
- Nicolas Meric
- Frédéric Voisin
- Burkhart Wolff
- Adrien Durier
- Natalia Kushik
Presentators
- Robert Sachtleben, Uni-Bremen, Germany
Summary:
Complete test suites are of special interest in the field of model-based testing, as they guarantee high fault detection capabilities. The variety and complexity of proposed strategies, their implementations, and their corresponding completeness arguments, however, impede thorough manual verification and practical employment.
We present a novel approach to the verification and synthesis of such strategies for models specified using finite state machines. First, we unify the presentation of several such strategies into a single framework implemented as a higher order function, which represents their shared high-level behaviour. Next, we model this framework in the interactive theorem prover Isabelle. Completeness proofs over frameworks are decoupled from concrete implementations of their parameters by suitable interfaces. This approach enables the reuse of proofs between similar strategies and simplifies implementations and completeness proofs of new variations on already handled strategies. Finally, we generate provably correct implementations of the considered test strategies. It is shown that these exhibit comparable performance to a manually developed C++ library for certain inputs.
This test-club meeting served for an in-depth discussion of the LMF seminar yesterday including demos and a discussion of the formal theory architecture as well as the code gerneration aspects and finally practical issues in using the tool.
Major Points :
A high-flying pass through the theory:
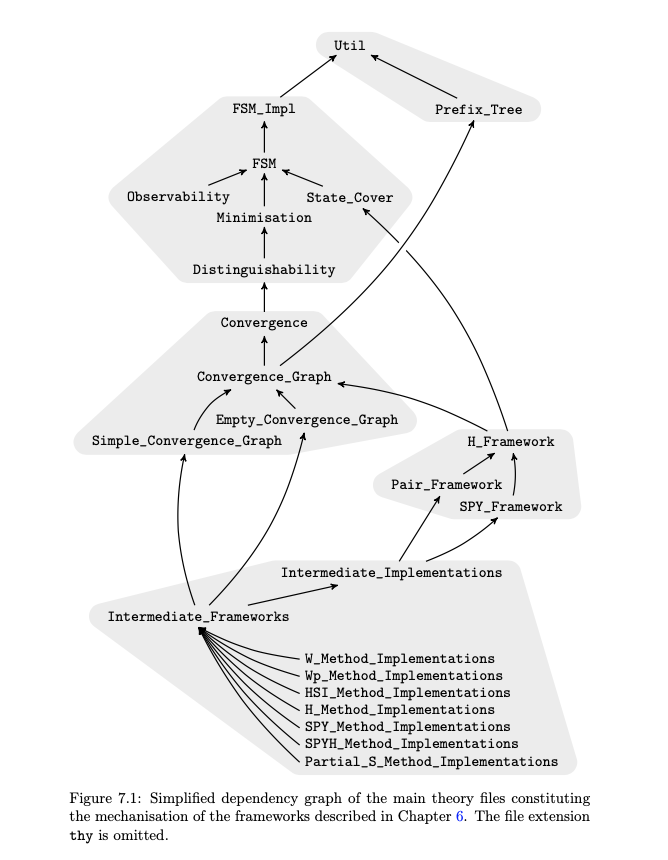
The upper part is a (fragment od) classical automata theory, then a formalisation of fiat state machines (FSM) and finally the formalisations of the frameworks, together with proofs of correctness and completeness.
A longer discussion comes into play: Where does actually non-determinism comes into play in code-generation? Where is actually the potential to improve complexity when the theory assumes ab-initio deterministic observable machines ? (Natalia claims that many non-deterministic observable machine can be converted into a deterministic one; Robert answers that this is not possible without changing outputs conceptually into inputs). Roberts claims that the data-structures are the same, but the data set is smaller. Natalia asks if all methods are capable of dealing with the non-deterministic machine ? The answer is yes:
Both C++ Implementations are specialised to completely specified deterministic FSMs, i.e. that each pair (q,x) consisting of a state and an input is mapped to exactly one paar (y,q') consisting of output and successor state. This means that it suffices to base all computations on input sequences, since reached states and produced outputs are uniquely defined.
Roberts implementations fon´t use this specialisations and work internally with IO-sequences, which results in significantly larger representations of test-suites in general. Robert did not investigate the impact of a specialisation of the implementations in more detail.
Demos:

So the the data-structures are the same, but the data set is smaller
NK: 1) Are all methods capable of dealing with the non-deterministic machine ? YES Tried to think about it over the night... But still maybe missing something - why exactly the Isabelle implementation "wins" again the C++ one ? What's the trick ?
Reason: The data-structure uses simpler (naive) data -structure . More interesting question: why are in Roberts implementation actually LESS test cases generated ? Where stems the redundancy in the classical approaches come from ?
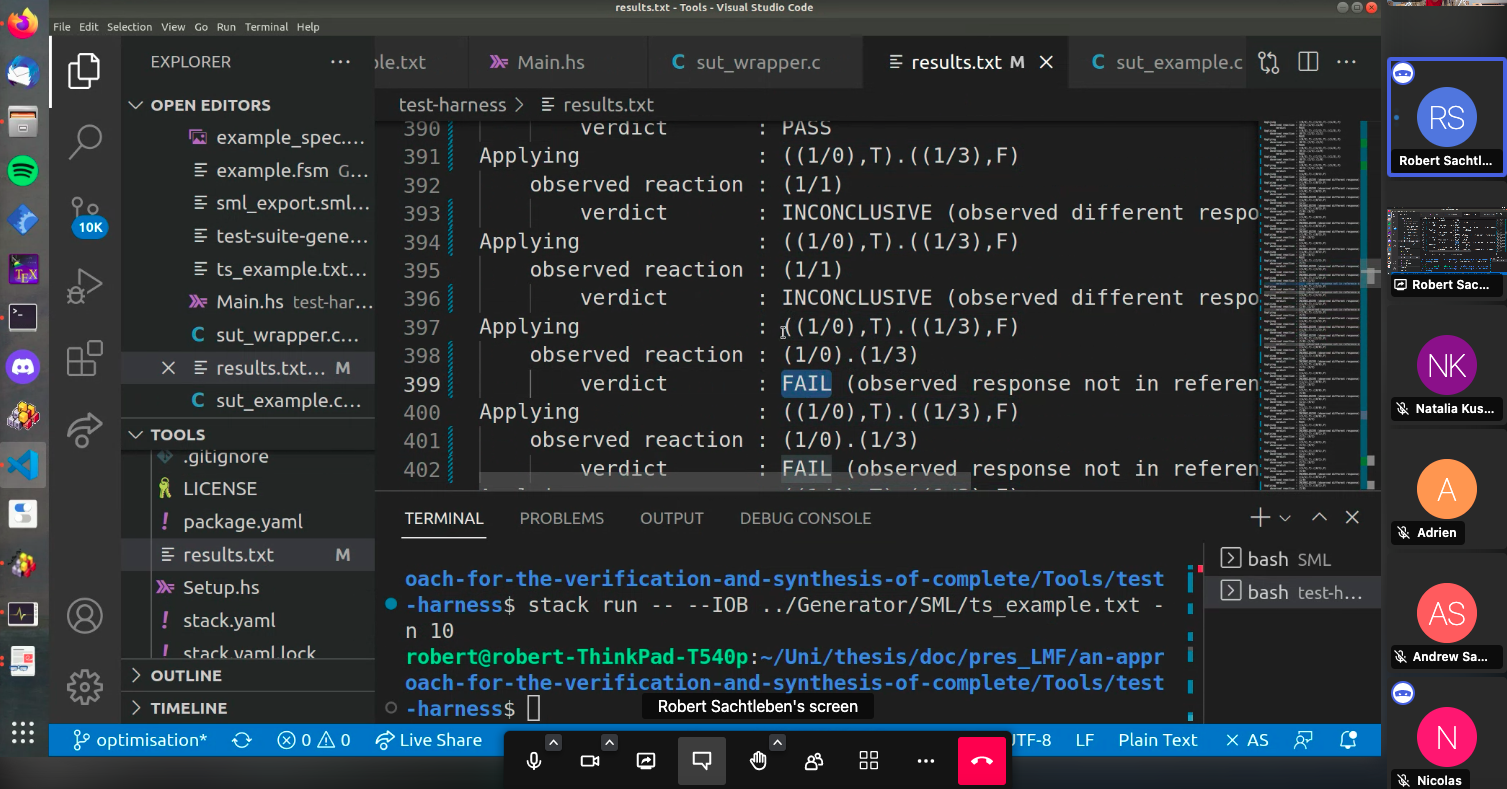
Less but Longer ? DATA to be collected.
Which part of the definitions could not be code generated / code-equations MOST worked out of the box due to FINITENESS of state machines of sequences. Few had to be rewritten.
How were optimizations measured?
Most cases obvious, otherwise profiling on sample automata, comparing entire tools on a data-set.
The harness is implemented externally in Haskell for pragmatical reasons.
Possible extensions
Generating Checking sequences to avoid initialisations and reduce the test-sets further (test1 + homing1 + test2 + homing2 + ... + test * homing).