Public iCal link: https://calendar.google.com/calendar/ical/proval%40lri.fr/public/basic.ics
Seminars
On Dependent Variables in Reactive Synthesis
Speaker: Supratik Chakraborty, IIT Bombay
Tuesday 10 June 2025, 14:00, Room 1B36 ENS Paris-Saclay
Abstract:

Given a Linear Temporal Logic (LTL) formula over input and output variables, reactive synthesis requires us to design a deterministic Mealy machine that gives the values of outputs at every time step, such that the LTL formula is satisfied. In this talk, we investigate the notion of dependent outputs in the context of reactive synthesis. Inspired by successful pre-processing techniques in Boolean functional synthesis, we define dependent outputs in reactive synthesis as outputs that are uniquely determined, given an assignment to all other variables and the history so far. We describe an automata-based approach for finding a set of dependent outputs. Using this, we show that dependent outputs are surprisingly common in reactive synthesis benchmarks. Next, we develop a novel framework that exploits dependent outputs in solving a synthesis problem. By implementing this framework using the widely used library Spot, we show that reactive synthesis that exploits dependent variables can solve some problems beyond the reach of existing techniques. Furthermore, we observe that among benchmarks with dependent outputs, if the count of non-dependent variables is low (≤ 3 in our experiments), our method outperforms state-of-the-art tools for synthesis.
This is joint work with S. Akshay, Eliyahu Basa and Dror Fried, and appeared in TACAS 2024.
Bio:
Supratik Chakraborty is Bajaj Group Chair Professor of Computer Science and Engineering at IIT Bombay. His research interests lie at the intersection of theoretical and applied computer science, with a focus on scalable and practical formal methods. He is a Fellow of Indian National Academy of Engineering and a Distinguished Member of ACM.
Planning
Past seminars
KEYNOTE : The Role of Logic in Advancing Machine Learning: Three Case Studies
Speaker: Pablo Barcelo, Chair of Computational Engineering, School of Engineering and Faculty of Mathematics, Universidad Católica de Chile
Tuesday 20th May 2025, 14:00, 1Z56 (to be confirmed)
Abstract:

I present three case studies from my collaborative research that highlight the essential role of logic in enhancing our understanding of modern machine learning architectures. The first two examples focus on the expressive capabilities of two prominent architectures: Transformers, which have revolutionized NLP applications, and Graph Neural Networks, a leading approach for classifying graph-structured data. We employ temporal logic techniques to analyze the properties that Transformers can recognize, and modal logics to examine the properties discernible by Graph Neural Networks. The third example addresses the pursuit of explainable AI, demonstrating how first-order logic can be used to design languages that declare, evaluate, and compute explanations for decisions made by machine learning models.
Regular Grammars for Sets of Graphs of Tree-Width 2
Speaker: Radu Iosif, CNRS/VERIMAG, Rhones des Alpes
Tuesday 29th April 2025, 14:00, 1Z56
Abstract:
Regular word grammars are context-free grammars having restricted rules, that define all recognizable languages of words. This paper generalizes regular grammars from words to certain classes of graphs, by defining regular grammars for unordered unranked trees and graphs of tree-width 2 at most. The qualifier ``regular'' is justified because these grammars define precisely the recognizable (equivalently, CMSO-definable) sets of the respective graph classes. The proof of equivalence between regular and recognizable sets of graphs relies on the effective construction of a recognizer algebra of size doubly-exponential in the size of the grammar. This sets a 2EXPTIME upper bound on the (EXPTIME-hard) problem of inclusion of a context-free language in a regular language, for graphs of tree-width 2 at most. A further syntactic restriction of regular grammars suffices to capture precisely the MSO-definable sets of graphs of tree-width 2 at most, i.e., the sets defined by CMSO formulae without cardinality constraints. Moreover, we show that MSO-definability coincides with recognizability by algebras having an aperiodic parallel composition semigroup, for each class of graphs defined by a bound on the tree-width.
This is joint work with Marius Bozga (Verimag) and Florian Zuleger (TU Wien).
Guiding a monkey in an infinite tree, adding new strategies for proof automation to the Tamarin prover
Speaker: Maiwenn Racouchot, Loria (Nancy), CISPA
Tuesday 2025-03-04 14:00, 1Z62
Abstract: Tamarin-prover is a tool for symbolic modeling and analysis of security protocols. It takes as an input a protocol's model, specifying the roles of the different agents (initiator, responder, different attacker models...) and some security properties required by the protocol. Tamarin can simulate an unbounded number of sessions running in parallel, which means an infinite number of role instances and possible fresh numbers. The execution of the different roles gives a transition system. The security properties are written as trace properties that will be matched against the transition system. To conduct proofs, Tamarin includes by default eight static heuristics. They help cover most cases, but can sometimes be really inefficient. In order to deal with these cases, Tamarin allows its users to create personalized heuristics by writing a script in a foreign programing language (usually python). However, this functionality has several limits (limited input information, state agnostic, compatibility issues). Moreover, while going through the proof tree, Tamarin can get stuck in a loop which prevents the proof from finishing. In this presentation, I will present several tools and approaches to improve Tamarin termination, from a new heuristic language to loop detection and bounded explorations for attack finding. I will also show how these new tools can be combined for greater results.
KEYNOTE: Alpha-Beta Pruning Explored, Extended and Verified
Speaker: Tobias Nipkow, Technische University München (Emeritus)
Tuesday 2025-03-11 14:00, 1Z76
Abstract:
Alpha-beta pruning is an efficient search strategy for two-player game trees. It was invented in the late 1950s and is at the heart of most implementations of combinatorial game playing programs. In this talk I will survey my recent formalizations and verifications of a number of standard variations of alpha-beta pruning. Findings include:
- Basic variants already having a property ascribed to an improved version
- Authors being confused about which algebraic structure they actually work in
- Generalizations to new algebraic structures
- The implementation in a famous paper is flawed
KEYNOTE : Formal Methods for Modern Payment Protocols
Speaker: David Basin, Prof. Dr . David Basin, Chair of the Computer Security Group, ETH Zürich
Tuesday 8th April 2025, 14:00, 1 Z 18 (Salle d'Alembert)
Abstract: EMV is the international protocol standard for smartcard payments and is used in billions of payment cards worldwide. Despite the standard’s advertised security, various issues have been previously uncovered, deriving from logical flaws that are hard to spot in EMV’s complex specification, running over 2,000 pages.

We have formalized various models of EMV in Tamarin, a symbolic model checker that we developed for cryptographic protocols. Tamarin was extremely effective in finding critical flaws, both known and new. For example, we discovered multiple ways that an attacker can use a victim's EMV card (e.g., Mastercard or Visa Card) for high-valued purchases without the victim's supposedly required PIN. Said more simply, the PIN on your EMV card is useless! We report on this, as well as followup work with an EMV consortium member on verifying the latest, improved version of the protocol, the EMV Kernel C-8. Overall our work provides evidence that security protocol model checkers like Tamarin have an essential role to play in developing critical, real-world cryptographic protocols, and that they are up to this challenge.
Formalised meta-theory for a certified type-theoretic kernel
Speaker: Meven LENNON-BERTRAND, University of Cambridge,mgapb2@cam.ac.uk
Tuesday 2024-12-17 14:00, Room to be announced
Abstract:
Proof assistant kernels are a natural target for program certification: they are critical, yet small and well-specified. Still, despite the maturity of type theory and software verification, we are yet to see a certified Agda, Coq or Lean. In my talk, I will give an overview of the landscape around this grand goal, more particularly of the interaction between certification and meta-theory, and present two complementary formalisation projects in that direction.
The core difficulty is that kernels rely on complex invariants, which in turn rest on significant properties of the type system. In essence, we cannot certify a kernel without first formalising the meta-theory of its type system. Historically, emphasis has been put on the *normalisation* property. I will explain why, in my view, other properties are more important, in particular the one called *injectivity of type constructors*.
Strict Categories with Families
Speaker: Loic Pujet, University of Stockholm, loic@pujet.fr
Tuesday 26 Nov 2024, 14:00, Room 1Z56
Abstract:

Categories with families (CwF) are perhaps the most widely used notion of models for dependent types. They can be described by an algebraic signature with dependent sorts for contexts, substitutions, types and terms, as well as a plethora of constants and equations. Unfortunately, this mix of dependent sorts and equations is particularly prone to transport hell, and in practice it is nearly impossible to prove non-trivial results using CwFs in a proof assistant.
In this talk, I will present a method based on Pédrot's "prefascist sets" to strictify (nearly) all the equations of a CwF, so that they hold by definition. I will then discuss applications of this method to formal proofs of canonicity and normalisation.
This is joint work with Ambrus Kaposi.
Lindenmayer graph languages, first-order theories and expanders
Speaker: Teodor Knapik, Université de la Nouvelle-Calédonie, Nouméa
Tuesday 14 May 2024, 14:00, Room 1Z56
Abstract: Imagined by Kolmogorov in the middle of past century, expanders form remarkable graph families with applications in areas as diverse as robust communication networks and probabilistically checkable proofs, to name just two. Since the proof of the existence of expanders, it took several years to come up with an explicit algebraic construction [Margulis 1973] of some expander families. Their first elementary (combinatorial) construction has been published in 2002 and awarded Gödel Prize in 2009.
In this talk, we introduce a framework that captures most of the known combinatorial constructions of expanders. It is based on a generalisation of Lindenmayer systems to the domain of graphs. We call this formalism Lindenmayer graph grammars. We identify a few essential properties which make decidable the language checking problem with respect to first-order sentences. This result is obtained by encompassing a graph language into an automatic structure. By language checking in this specific context, we mean the following problem.
Instance: a Lindenmayer graph grammar and a first-order sentence. Question: Does there exist a graph in the language for which the sentence holds?
Keynote: Challenges and triumphs of verification in the CSP style
Speaker: Bill Roscoe Emeritus professor, University of Oxford, GB
Thursday (!) May 23 2024, 14:00, Room 1Z56

Abstract: I have been doing practical verification in CSP, its tools and models for 40 years. The main challenge has been packaging this for the industrial engineer. I will discuss how this has been solved in the Coco System www.cocotec.io, which is used for object based development of massive systems in industry. Separately I will show how I have used it to underpin a highly innovative blockchain consensus protocol by using it to model decentralised, partly malevolent systems.
Static analysis and model reduction for a site-graph rewriting language
Speaker: Jérôme Feret ENS Ulm, jerome.feret@ens.psl.eu
Tuesday Mar 26 2024, 14:00, Room 1Z56
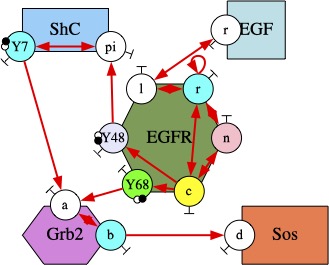
Abstract: Software sciences have a role to play in the description, the organization, the execution, and the analysis of the molecular interaction systems such as biological signaling pathways. These systems involve a huge diversity of bio-molecular entities whereas their dynamics may be driven by races for shared resources, interactions at different time- and concentration-scales, and non-linear feedback loops. Understanding how the behavior of the populations of proteins orchestrates itself from their individual interactions, which is the holy grail on systems biology, requires dedicated languages offering adapted levels of abstraction and efficient analysis tools.
In this talk we describe the design of formal tools for Kappa, a site-graph rewriting language inspired by bio-chemistry. In particular, we introduce a static analysis to compute some properties on the biological entities that may arise in models, so as to increase our confidence in them. We also present a model reduction approach based on a study of the flow of information between the different regions of the biological entities and the potential symmetries. This approach is applied both in the differential and in the stochastic semantics.



