Speaker: Cameron Calk https://ccalk.github.io/, LIS / Aix-Marseille University Room 1Z25 (Zoom link)
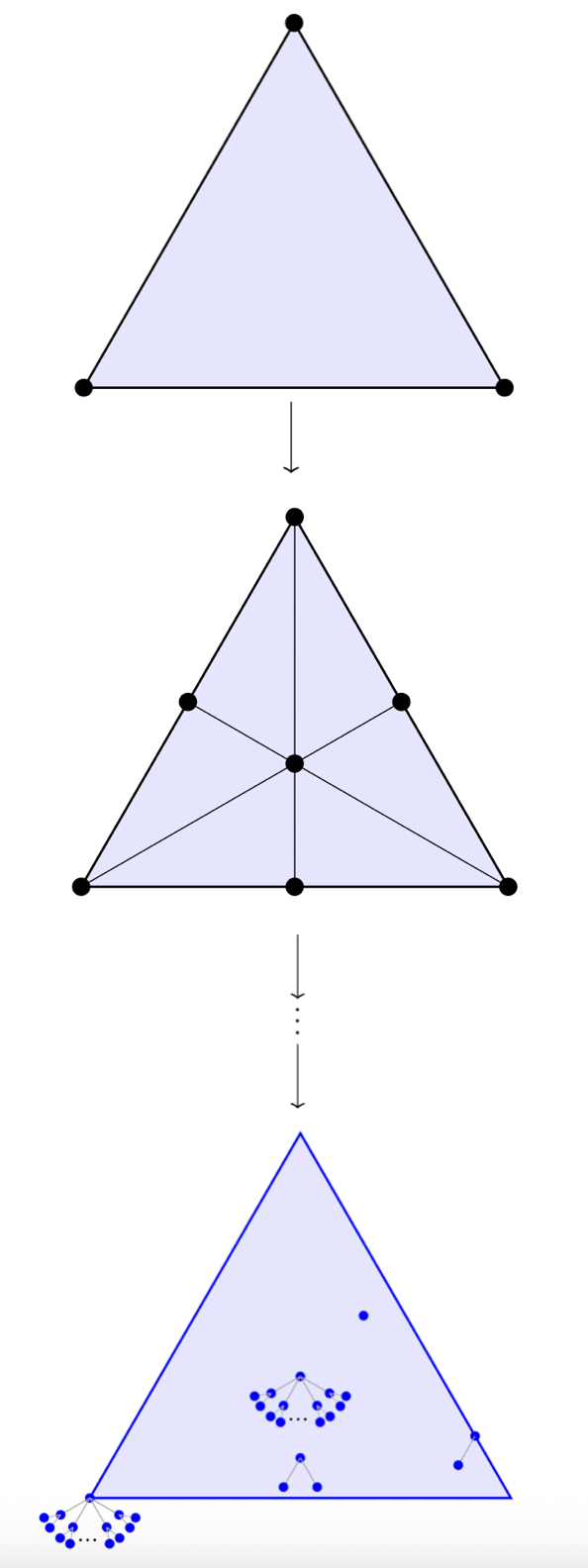
Abstract: An important question in the domain of distributed computing is that of task solvability : given a distributed task, the analog of a program specification for distributed systems, under which conditions can it be solved by some distributed protocol ? The topological approach to distributed computing represents tasks and protocols as relations between simplicial complexes, combinatorial objects which encode possible global states of the system. These have a spatial interpretation, which led to the Asynchronous Computability Theorem (ACT), which relates, for certain computational models, the existence of a continuous map to task solvability, using subdivisions of the input space.
In this talk, I will present a generalisation of the ACT for colourless protocols based on categorical and duality theoretic constructions. This is achieved by viewing an iterated protocol as an endofunctor on the category of simplicial complexes, along with a natural transformation encoding the relation between inputs and computational outputs. From this data we produce, for each possible set of inputs, a limit object in the form of a spectral space which encodes all possible computational outputs, and characterises the task solvability of the protocol. Indeed, a protocol can solve a task if, and only if, there exists a continuous map from the associated spectral space to the space of outputs. This construction works for any iterated protocol, but we additionally show that it is compatible with the original approach using subdivision protocols, since in this case the geometric realisation, the space used in the original ACT, is a canonical subspace of the associated spectral space.
This is a joint work with Emmanuel Godard, and a pre-print can be found on arXiv here.



